[This is a note, which is the seed of an idea and something I’ve written quickly, as opposed to articles that I’ve optimized for readability and transmission of ideas.]
I further expand on the ideas I introduced in Bayesian information theory.
$$
\newcommand{\0}{\mathrm{false}}
\newcommand{\1}{\mathrm{true}}
\newcommand{\mb}{\mathbb}
\newcommand{\mc}{\mathcal}
\newcommand{\mf}{\mathfrak}
\newcommand{\and}{\wedge}
\newcommand{\or}{\vee}
\newcommand{\es}{\emptyset}
\newcommand{\a}{\alpha}
\newcommand{\t}{\tau}
\newcommand{\T}{\Theta}
\newcommand{\D}{\Delta}
\newcommand{\o}{\omega}
\newcommand{\O}{\Omega}
\newcommand{\x}{\xi}
\newcommand{\z}{\zeta}
\newcommand{\fa}{\forall}
\newcommand{\ex}{\exists}
\newcommand{\X}{\mc{X}}
\newcommand{\Y}{\mc{Y}}
\newcommand{\Z}{\mc{Z}}
\newcommand{\P}{\Psi}
\newcommand{\y}{\psi}
\newcommand{\p}{\phi}
\newcommand{\l}{\lambda}
\newcommand{\B}{\mb{B}}
\newcommand{\m}{\times}
\newcommand{\E}{\mb{E}}
\newcommand{\N}{\mb{N}}
\newcommand{\I}{\mb{I}}
\newcommand{\H}{\mb{H}}
\newcommand{\e}{\varepsilon}
\newcommand{\set}[1]{\left\{#1\right\}}
\newcommand{\par}[1]{\left(#1\right)}
\newcommand{\vtup}[1]{\left\langle#1\right\rangle}
\newcommand{\abs}[1]{\left\lvert#1\right\rvert}
\newcommand{\inv}[1]{{#1}^{-1}}
\newcommand{\ceil}[1]{\left\lceil#1\right\rceil}
\newcommand{\dom}[1]{_{|#1}}
\newcommand{\df}{\overset{\mathrm{def}}{=}}
\newcommand{\M}{\mc{M}}
\newcommand{\up}[1]{^{(#1)}}
\newcommand{\Dt}{{\Delta t}}
\newcommand{\Dh}{{\Delta h}}
\newcommand{\tr}{\rightarrowtail}
\newcommand{\tra}[2]{\,^{#1\!\!}\searrow _{#2\,}}
\newcommand{\mi}[4]{\,^{#1\!\!}\searrow _{#2\,}\rightrightarrows ^{#3}\searrow _{#4\,}}
\newcommand{\absp}[1]{\abs{#1}^+}
\newcommand{\Bar}{\overline}
\newcommand{\dmid}{\,\|\,}
\newcommand{\V}[1]{\begin{pmatrix}#1\end{pmatrix}}
\require{cancel}
$$
We have a set of possibilities $\O$, and there is a true but unknown possibility $\o^*\in\O$. I define information as a tuple of the form $(\O,R)$ where $R\subseteq \O$, which asserts that $\o^*\in R$. I notate these information tuples with arrows:
$$
\O\tr R \df (\O, R)\,,
$$
which makes it clear that information is the narrowing-down of a possibility space.
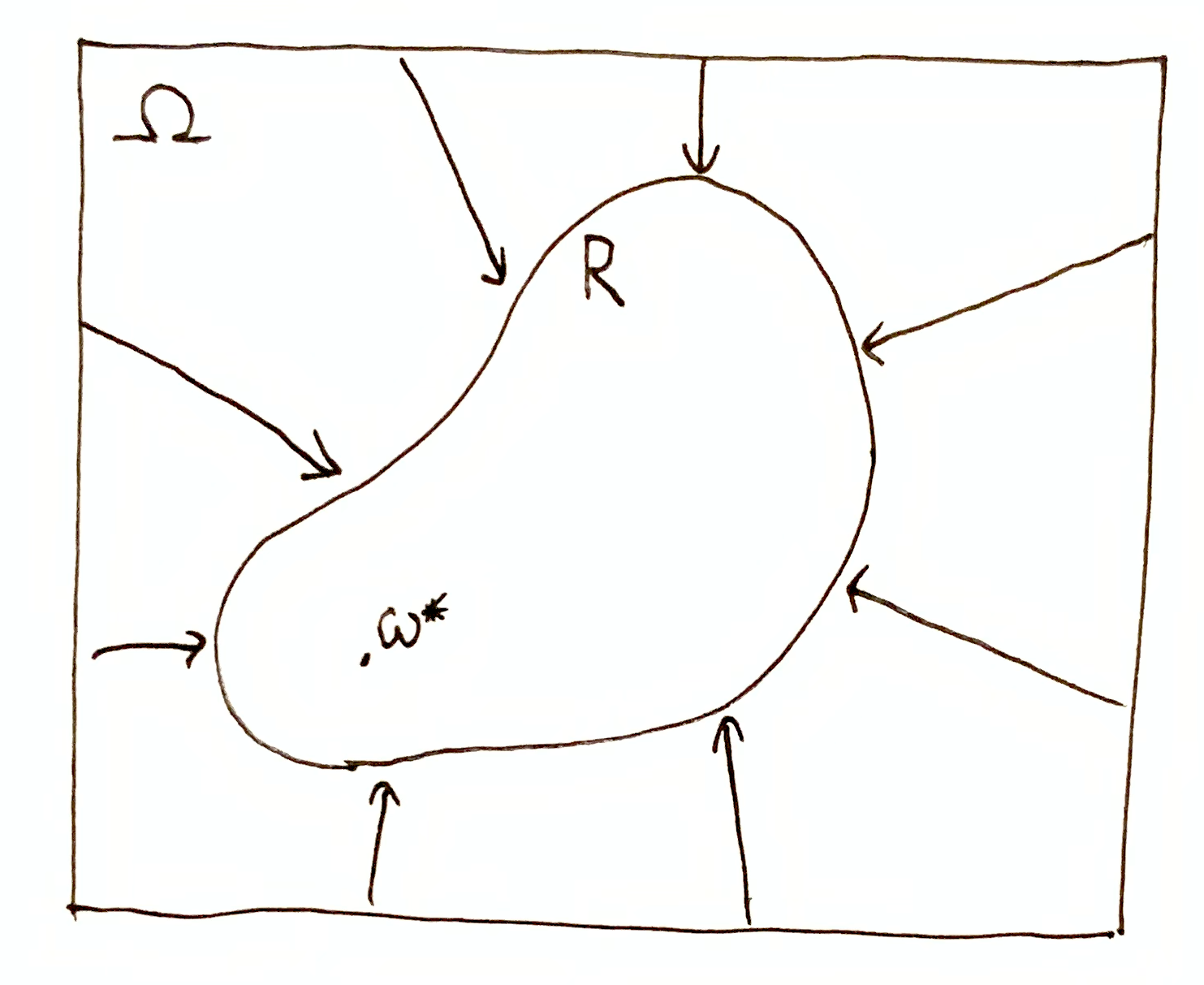
I also use the following notation for domain restriction:
$$
A\dom{B} \df A \cap B\,,
$$
which is the set $A$ restricted to the domain of $B$. This notation is more compact than intersection notation, and I can use it to emphasize the semantic distinction between which set is being restricted and which set is the domain.
To quantify information, we need a measure $\mu$ on $\O$. When $\O$ is finite, I always use the counting measure $\mu(A) = \abs{A}$. The measure $\mu$ need not be normalized on $\O$, i.e. $\mu(\O)$ need not be $1$. I interpret $\mu$ as just a measure of the size of regions of the possibility space, rather than a measure of probability or randomness.
The information $\O \tr R$ is quantified by
$$
h_\O(R) \df \lg\par{\frac{\mu(\O)}{\mu(R)}} = \lg\par{\frac{1}{\mu(R\mid \O)}}\,,
$$
which has the unit bits and measures the number of halvings it takes to go from $\O$ to $R$.
I put $\O$ in the subscript of $h$ to make it clear what the domain is. Let $\mu(A \mid B) \df \mu(A\dom{B} \mid B) = \mu(A\cap B\mid B)$ be the measure $\mu$ restricted to $B$ and normalized so that $\mu(B \mid B) = 1$. When $\mu(\O) = 1$, then $h_\O(R) = -\lg\mu(R)$ which is called self-information in Shannon’s information theory, and $h(A \mid B) = -\lg\mu(A \mid B)$ is called conditional self-information.
If $\O$ has already been narrowed down to $R$, and is then further narrowed down to $R'\subseteq R$, the incremental quantity of information, i.e. the quantity of $R\tr R'$, is given by $h(R' \mid R)$. In general, for any sets $A,B \subseteq \O$, the information $B \tr A\dom{B}$ is quantified by
$$
\begin{aligned}
h(A \mid B) &\df h_\O(A\dom{B}) - h_\O(B) \\
&= \lg\par{\frac{\mu(B)}{\mu(A\dom{B})}} \\
&= \lg\par{\frac{1}{\mu(A\mid B)}}\,.
\end{aligned}
$$
I leave off the $\O$ subscript because it has no bearing on this quantity. Note that $h(A \mid B) = h_B(A\dom{B}) = h_B(A\cap B)$ is just another way to specify the domain $B$. This is convenient notationally when $A\setminus B\neq \es$.
To make working with these quantities easier, I adopt the following shorthand:
$$
\begin{aligned}
h(B \tr A\dom{B}) &\df h(A\dom{B} \mid B) = h_B(A\dom{B}) \\
&= \lg\par{\frac{\mu(B)}{\mu(A\dom{B})}}\,.
\end{aligned}
$$
The lhs of the arrow goes in the numerator, and the rhs of the arrow goes in the denominator. This is convenient for thinking algebraically about more complex manipulations:
For $A \subseteq B$ and $B\subseteq C$,
$$
\begin{aligned}
h(C \tr B) + h(B \tr A) &= \lg\par{\frac{\mu(C)}{\cancel{\mu(B)}}} + \lg\par{\frac{\cancel{\mu(B)}}{\mu(A)}} \\
&= \lg\par{\frac{\mu(C)}{\mu(A)}} \\
&= h(C\tr A)\,.
\end{aligned}
$$
Likewise we obtain the following identities:
$$
\begin{aligned}
h(C\tr A) - h(B \tr A) &= h(C \tr B) \\
h(C \tr A) - h(C \tr B) &= h(B \tr A)\,.
\end{aligned}
$$
This successive narrowing down can be represented visually:
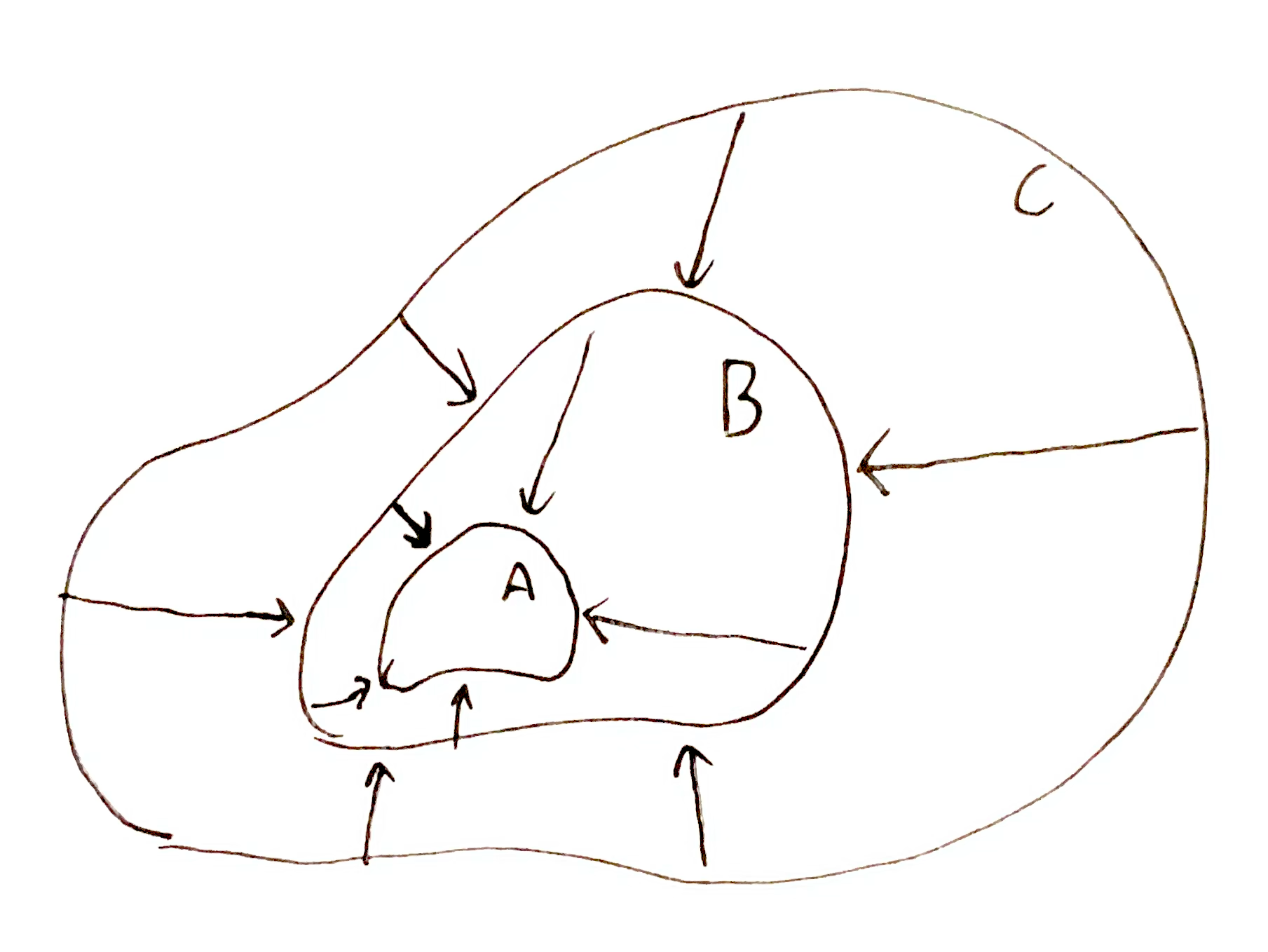
Mutual Information
Let $A,R\subseteq \O$. Suppose we have the information $\O\tr R$, corresponding to the knowledge that $\o^*\in R$. To be more succinct, I will say that we know that $R$ is true. Also suppose we don’t know whether $A$ is true, i.e. we don’t have the information $\O\tr A$. For information that is not known, I will use a small diagonal arrow, $\tra{\O}{A}$. We can think of this as aspirational information, i.e. information we do not have but would like to have.
Since $\tra{\O}{A}$ and $\O\tr A$ are mathematically equivalent, $h(\tra{\O}{A}) = h(\O\tr A) = \lg\frac{\mu(\O)}{\mu(A)}$.
Does $\O\tr R$ move us closer to the goal of $\tra{\O}{A}$? That is to say, given we have the information $\O\tr R$, what information about $A$ do we have? As we shall see, pointwise mutual information quantifies “information about”.
There are three ways $R$ and $A$ can interact:
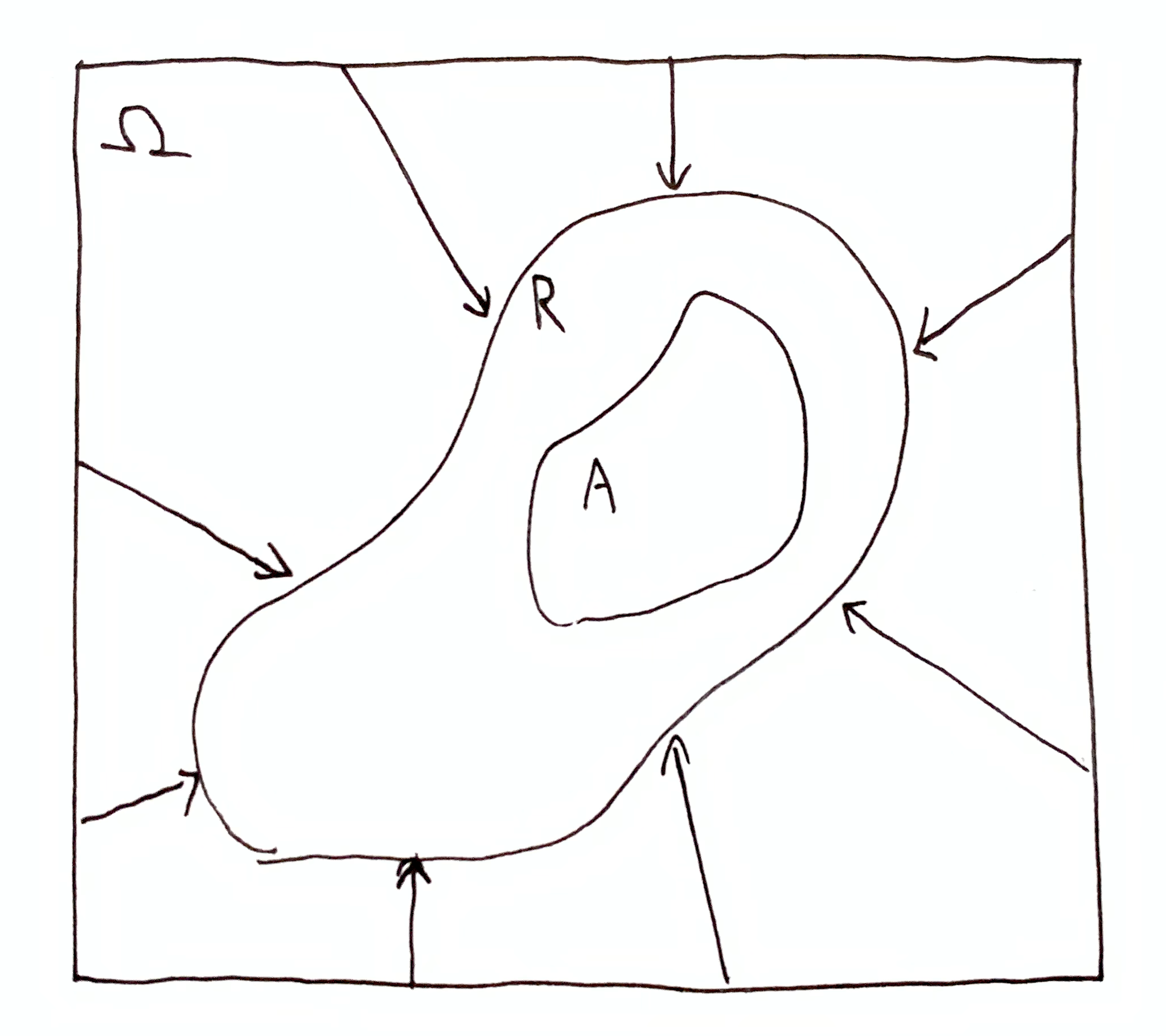
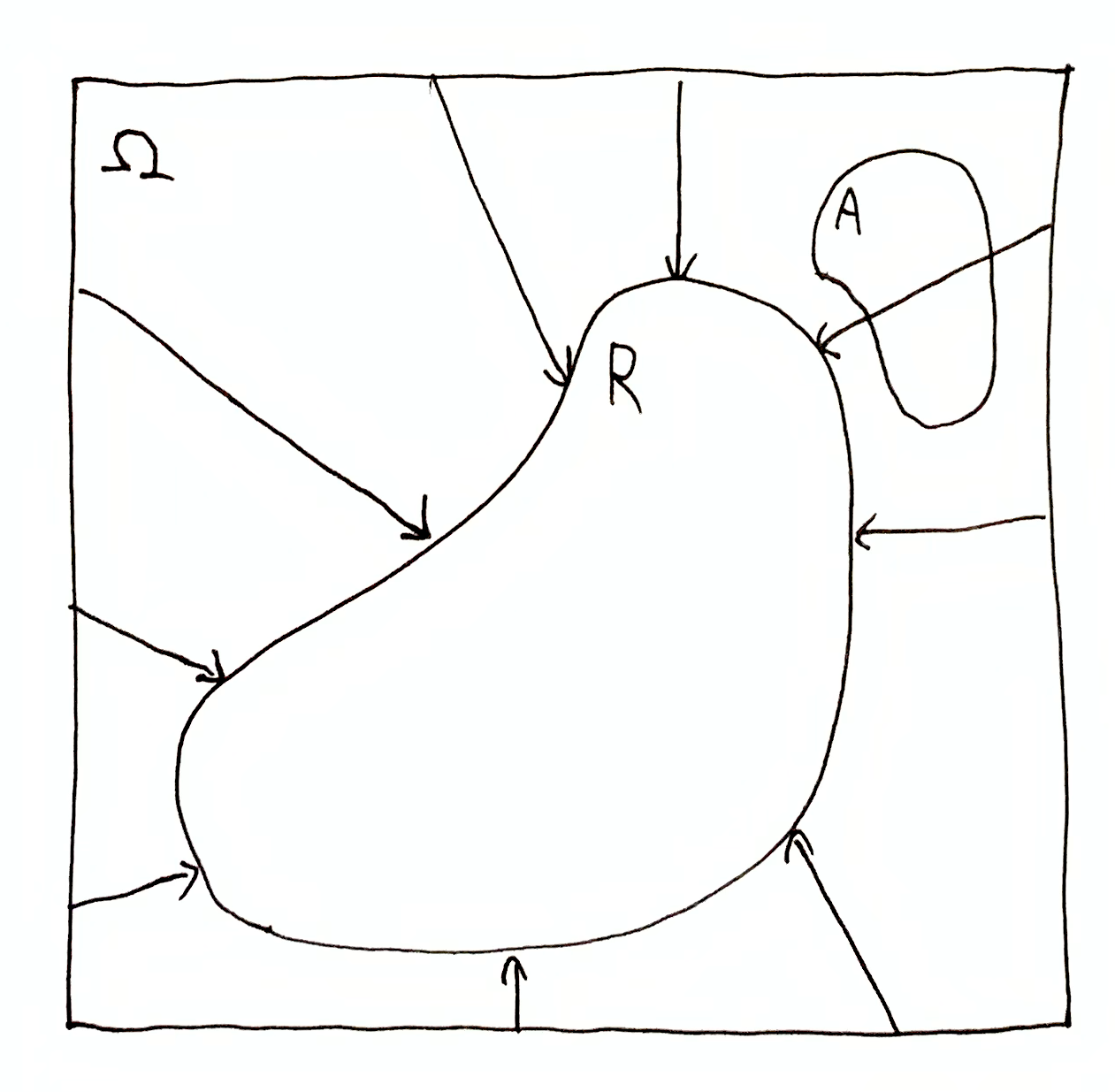
Arrows here indicate information we actually have, i.e. $\O\tr R$, and lack of arrows indicates information we don’t have, i.e. $\tra{\O}{A}$ and $\tra{R}{A\cap R}$.
In the first case, $A \subseteq R$, and $\tra{\O}{A}$ is transformed into $\tra{R}{A}$. Clearly $h(\tra{\O}{A}) - h(\tra{R}{A}) = h(\O\tr R)$ which is the quantity of information we have gained towards $\tra{\O}{A}$, and $h(\tra{R}{A})$ is the quantity of information still needed to know that $A$ is true.
In the other two cases, parts of $A$ are ruled out, which shrinks $A$ or reduces it to the empty set. The aspirational information $\tra{\O}{A}$ is transformed into $\tra{R}{A\dom{R}}$. The change in quantity is
$$
\begin{aligned}
h(\tra{\O}{A}) - h(\tra{R}{A\dom{R}}) &= \lg\par{\frac{\mu(\O)}{\mu(A)}} - \lg\par{\frac{\mu(R)}{\mu(A\dom{R})}} \\
&= \lg\par{\frac{\mu(A\dom{R})\mu(\O)}{\mu(A)\mu(R)}}\,,
\end{aligned}
$$
and nothing cancels out if $A \neq A\dom{R}$. This is an irreducible quantity of interest, called pointwise mutual information (PMI), formally defined as
$$
\begin{aligned}
i_\O(A, R) &\df \lg\par{\frac{\mu(A\dom{R})\mu(\O)}{\mu(A)\mu(R)}} \\
&= \lg\par{\frac{\mu(A \mid \O)}{\mu(A \mid R)}} \\
&= \lg\par{\frac{\mu(R \mid \O)}{\mu(R \mid A)}} \,.
\end{aligned}
$$
When $\mu(\O) = 1$ we get the more familiar expression, $i_\O(A, R) = \lg\par{\frac{\mu(A \cap R)}{\mu(A)\mu(R)}}$.
We can see that $i_\O(A, R)$ can also be written
$$
\begin{aligned}
i_\O(A, R) &= \lg\par{\frac{\mu(\O)}{\mu(R)}} - \lg\par{\frac{\mu(A)}{\mu(A\dom{R})}} \\
&= h(\O\tr R) - h(\tra{A}{A\dom{R}}) \\
&= i_\O(R, A)\,,
\end{aligned}
$$
where the $A$ and $R$ corners are swapped.
Since $h(\tra{A}{A\dom{R}})$ is always positive (because $\mu(A\dom{R})\leq\mu(A)$), we see that $i_\O(A, R)$ is upper bounded by $h(\O\tr R)$, and $i_\O(A, R) = h(\O\tr R)$ when $A \subseteq R$ (since $\mu(A\dom{R}) = \mu(A)$), which we previously derived.
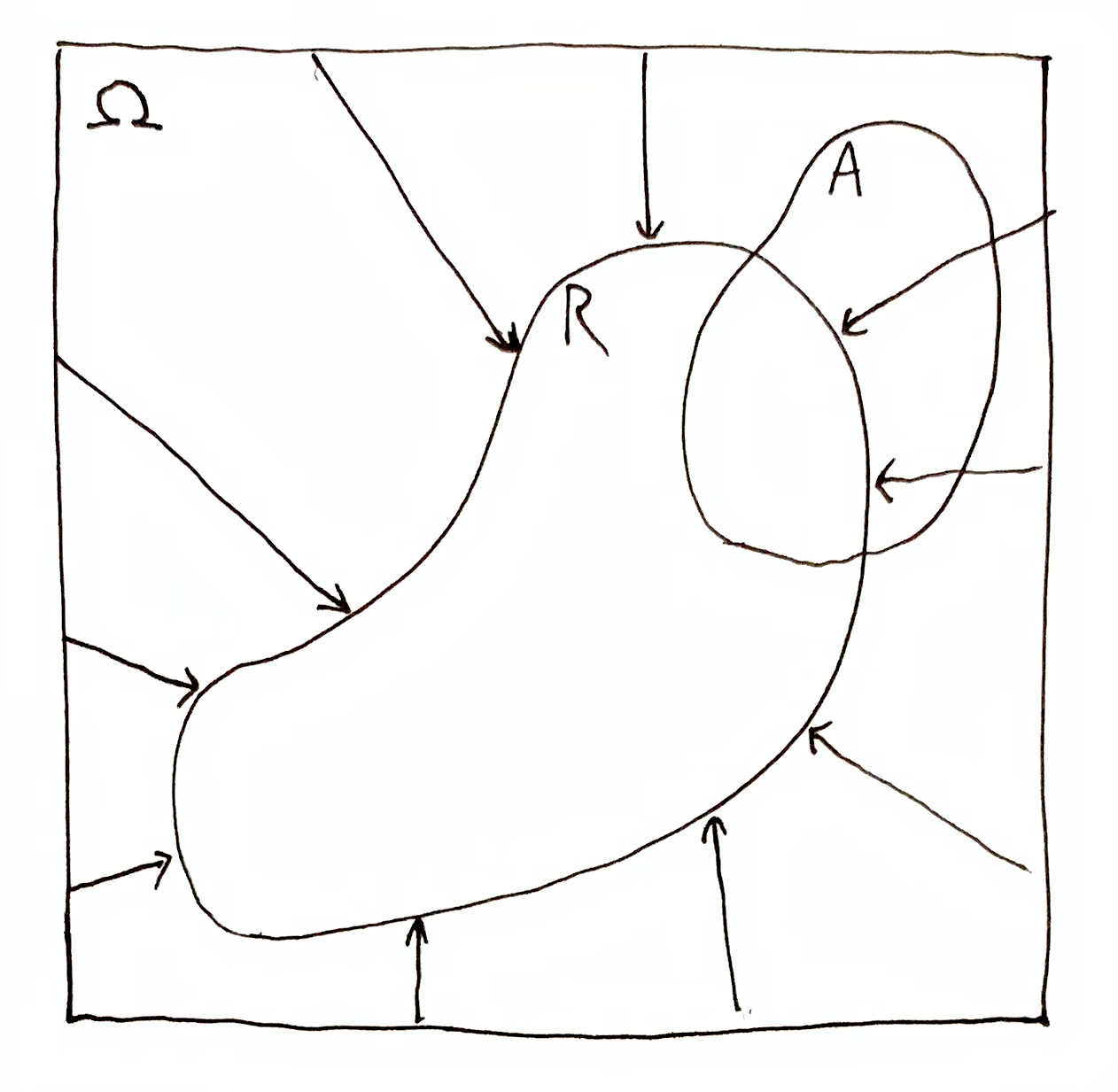
What about when $A\dom{R} \neq A$? It turns out that $i_\O(A, R)$ is not lower bounded, and can be arbitrarily negative. To interpret these negative values, let’s think about what is going on visually. The information $\O\tr R$ transforms $(\O,A)$ to $(R,A\dom{R})$:
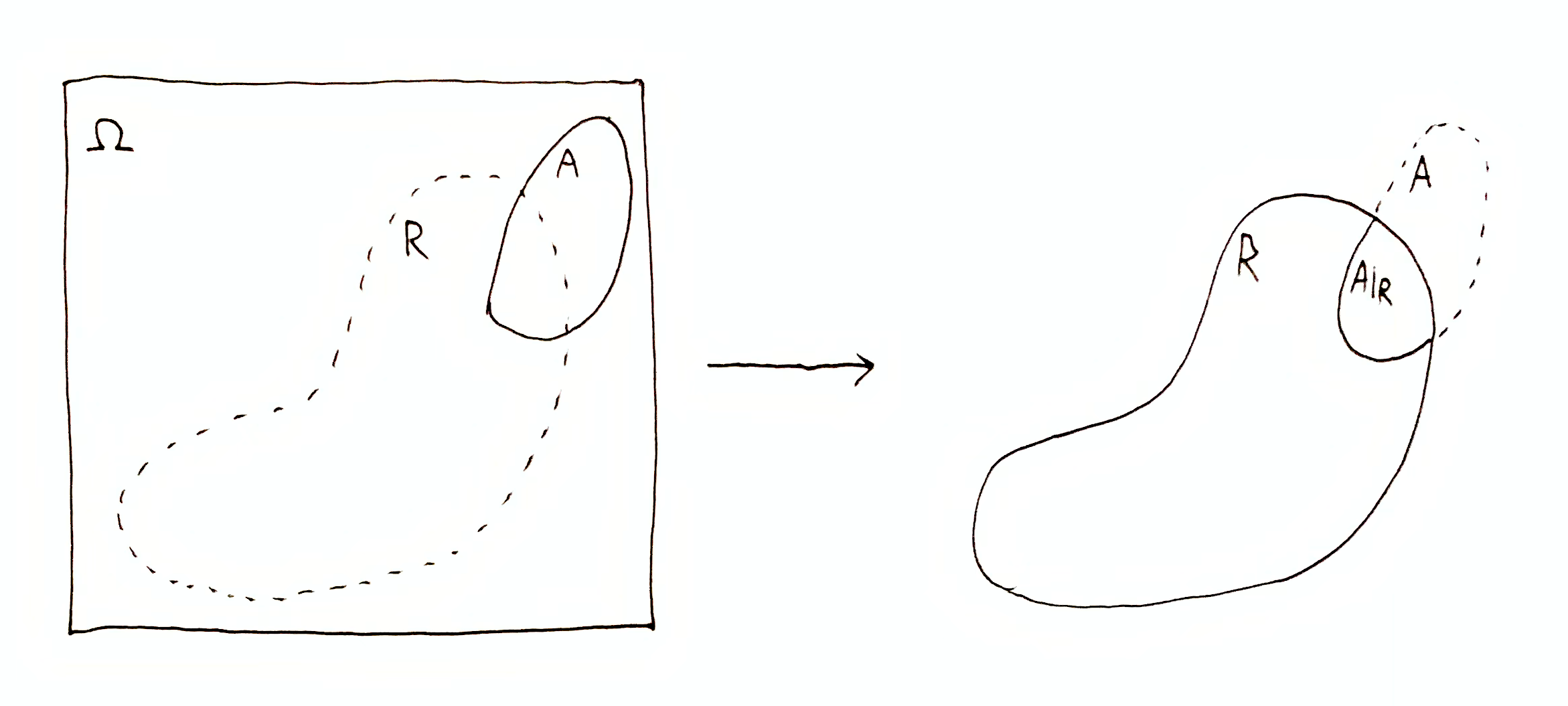
In terms of quantity, what has changed is the ratio: $\frac{\mu(\O)}{\mu(A)}$ to $\frac{\mu(R)}{\mu(A\dom{R})}$. Specifically, if $\frac{\mu(\O)}{\mu(A)} \to \frac{\mu(R)}{\mu(A\dom{R})}$ is one halving, i.e. $\frac{\mu(R)}{\mu(A\dom{R})} = \frac{1}{2}\frac{\mu(\O)}{\mu(A)}$, then $i_\O(A, R) = \lg\par{\frac{\mu(\O)}{\mu(A)}\Big{/}\frac{\mu(R)}{\mu(A\dom{R})}} = \lg\par{\frac{\mu(\O)}{\mu(A)}\Big{/}\frac{1}{2}\frac{\mu(\O)}{\mu(A)}} = \lg(2) = 1$ bit.
A different way to think about it is
$$
\begin{aligned}
i_\O(A,R) &= \lg\par{\frac{\mu(\O)}{\mu(R)\frac{\mu(A)}{\mu(A\dom{R})}}} \\
&= \lg\par{\frac{\mu(\O)}{\nu(R)}}\,,
\end{aligned}
$$
where $\nu(Q)=\mu(Q)\frac{\mu(A)}{\mu(A\dom{R})}$ rescales the size of any set $Q$ so that $\nu(A\dom{R}) = \mu(A\dom{R})\frac{\mu(A)}{\mu(A\dom{R})} = \mu(A)$. In this form, $i_\O(A,R)$ looks like the quantity of information for $\O\tr R$, but where the numerator and denominator use different measures. This quantity of information can be negative, unlike $h(\O\tr R)$.
This rescaling can be visualized by drawing to scale the relative proportions of $\mu(\O)$ and $\mu(A)$, and show below that the same relative proportions of $\nu(R)$ and $\nu(A\dom{R})$, so that $\nu(A\dom{R})$ is visually the same size as $\mu(A)$:
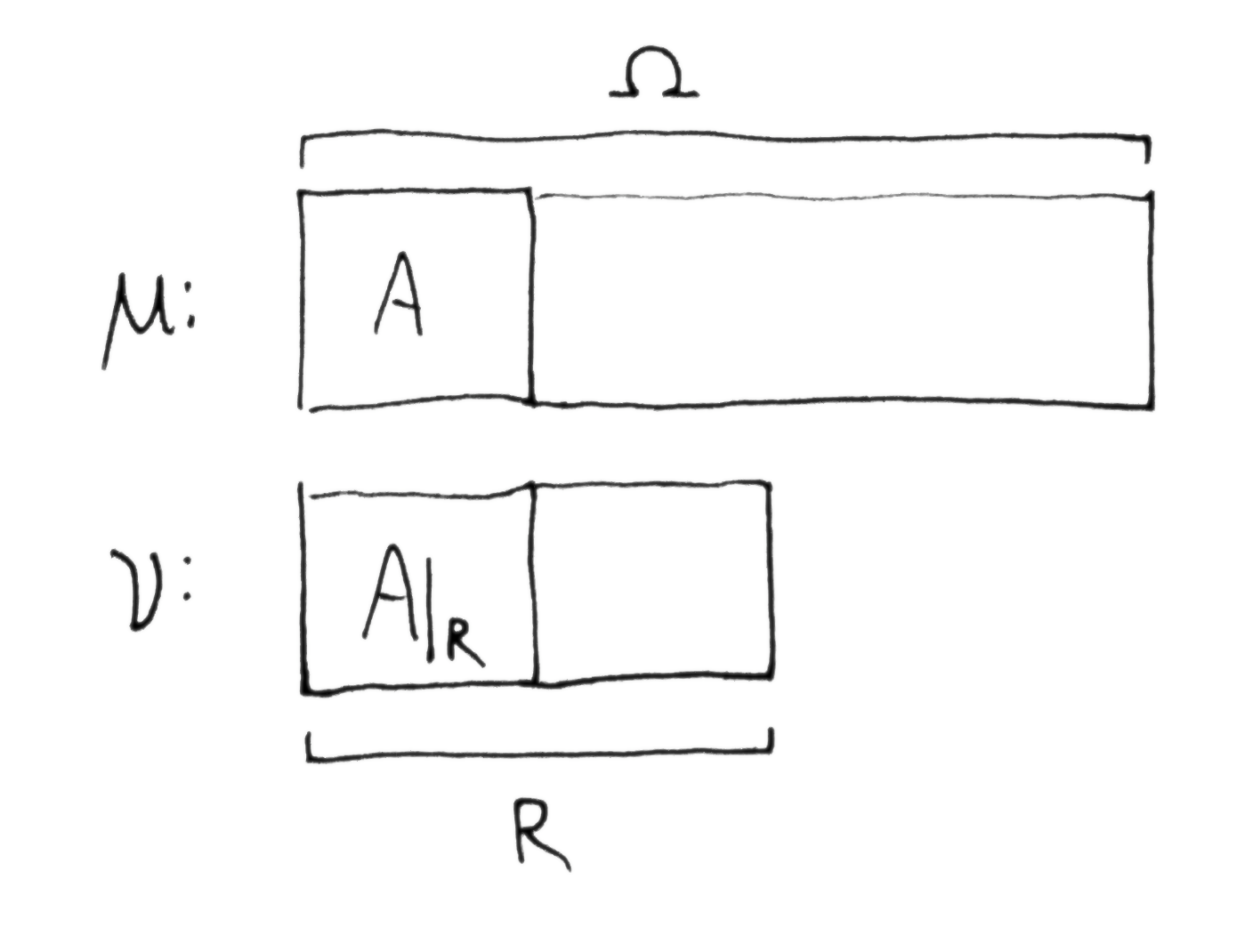
Here lengths denote size. This image shows that 1 bit is gained about whether $A$ is true because the domain is halved, i.e. we are 1 bit closer to knowing that $A$ is true. However, the bottom rectangle is rescaled so that $A$ and $A\dom{R}$ are visually the same size. $h(\O\tr R)$ may not be 1.
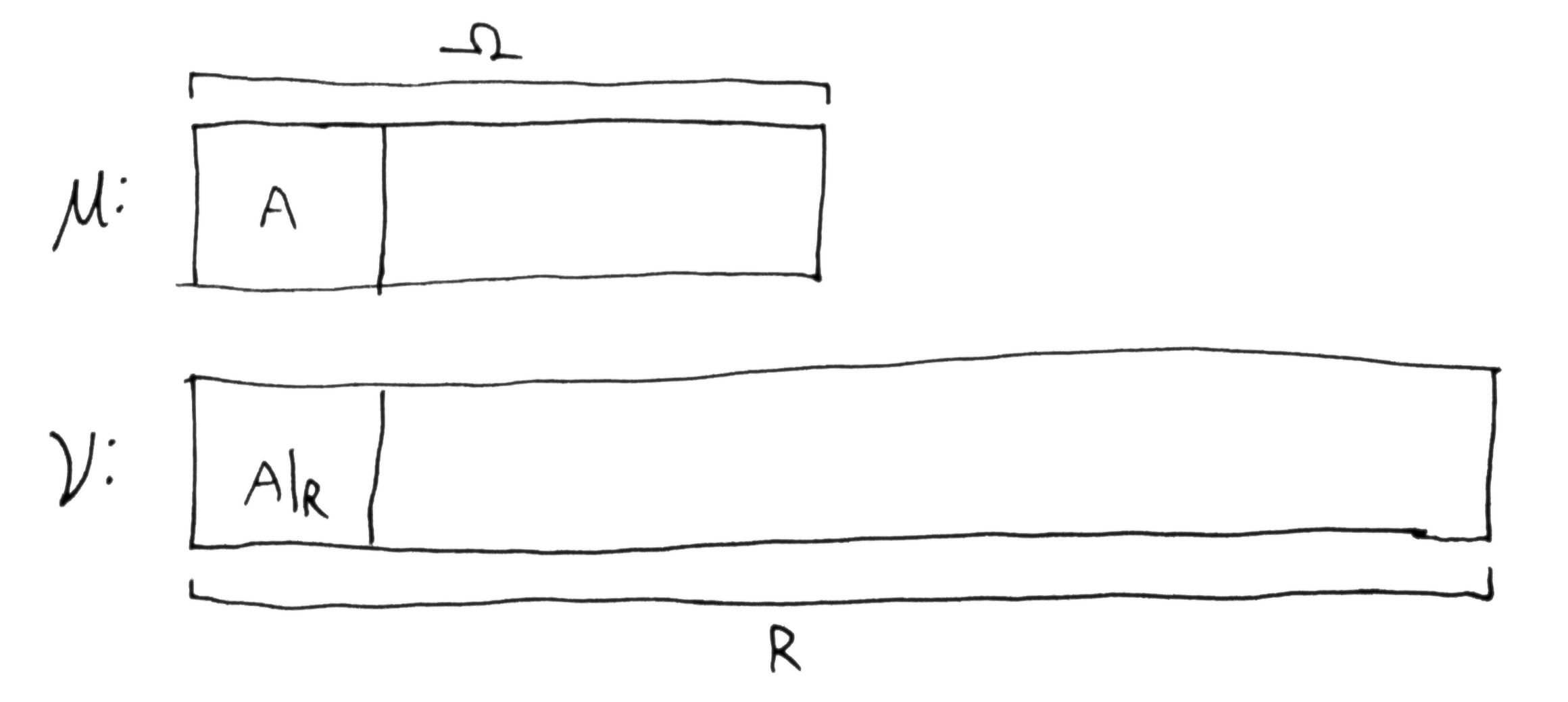
Here is another example where the narrowing down $\tra{A}{A\dom{R}}$ outpaces the narrowing down $\O\tr R$, i.e. more of $A$ is ruled out than the domain of $A$ is reduced. We see that this scaled domain appears to be doubled, which is the loss of 1 bit, i.e. $i_\O(A,R) = -1$. We are 1 bit further away from knowing that $A$ is true, and we now need an additional bit of information to know $\tra{\O}{A}$ compared with before $\O\tr R$ was known (compared with total ignorance).
Now we see why PMI is upper bounded but not lower bounded. At most, $i_\O(A, R) = h(\O\tr A)$ if $R = A$, which is equivalent to gaining the information that $A$ is true. This can be achieved in a finite number of halvings. On the other hand, the scaled domain of $A\dom{R}$ can grow arbitrarily large as $R$ rules out more and more of $A$, i.e. $\mu(A \setminus R) \to \mu(A)$ implies $\mu(A\dom{R}) \to 0$. If $A \cap R = \es$, then $i_\O(A,R) = -\infty$, which we can interpret to mean that $\O\tr R$ proves that $A$ is false, i.e. the knowledge that $\o^* \notin A$. Thus no amount of information can make $A$ true (an infinite quantity of information here indicates a contradiction).
PMI vs conditional information
$i_\O(A, R)$ and $h(A \mid R)$ are each quantifying a kind of transformation on $\tra{\O}{A}$. Assuming that $\O\tr R$ is already known,
- $i_\O(A, R)$ quantifies a change in the lhs (domain) and a rescaling of the rhs: $\tra{\O}{A} \to \tra{R}{A\dom{R}}$, whereas
- $h(A \mid R)$ quantifies a change in the rhs (target): $(\O\tr R) \to (\O \tr A)$, i.e. the amount of additional bits gained by this transformation.
A well known identity from information theory is $i_\O(A, R) + h(A \mid R) = h_\O(A)$, or written another way:
$$
i_\O(A, R) + h(R \tr A\dom{R}) = h(\O\tr A)\,.
$$
Why is this sum not equal to $h(\O\tr A\dom{R})$? Note that $h(\O\tr R) + h(R \tr A\dom{R}) = h(\O\tr A\dom{R})$. As we saw, $i_\O(A, R)$ is closely related to $h(\O\tr R)$ but not always the same.
The difference between $i_\O(A, R) + h(R \tr A\dom{R})$ and $h(\O\tr R) + h(R \tr A\dom{R})$ can be illustrated visually.
Double domain reduction $h(\O\tr R) + h(R \tr A\dom{R}) = h(\O\tr A\dom{R})$:
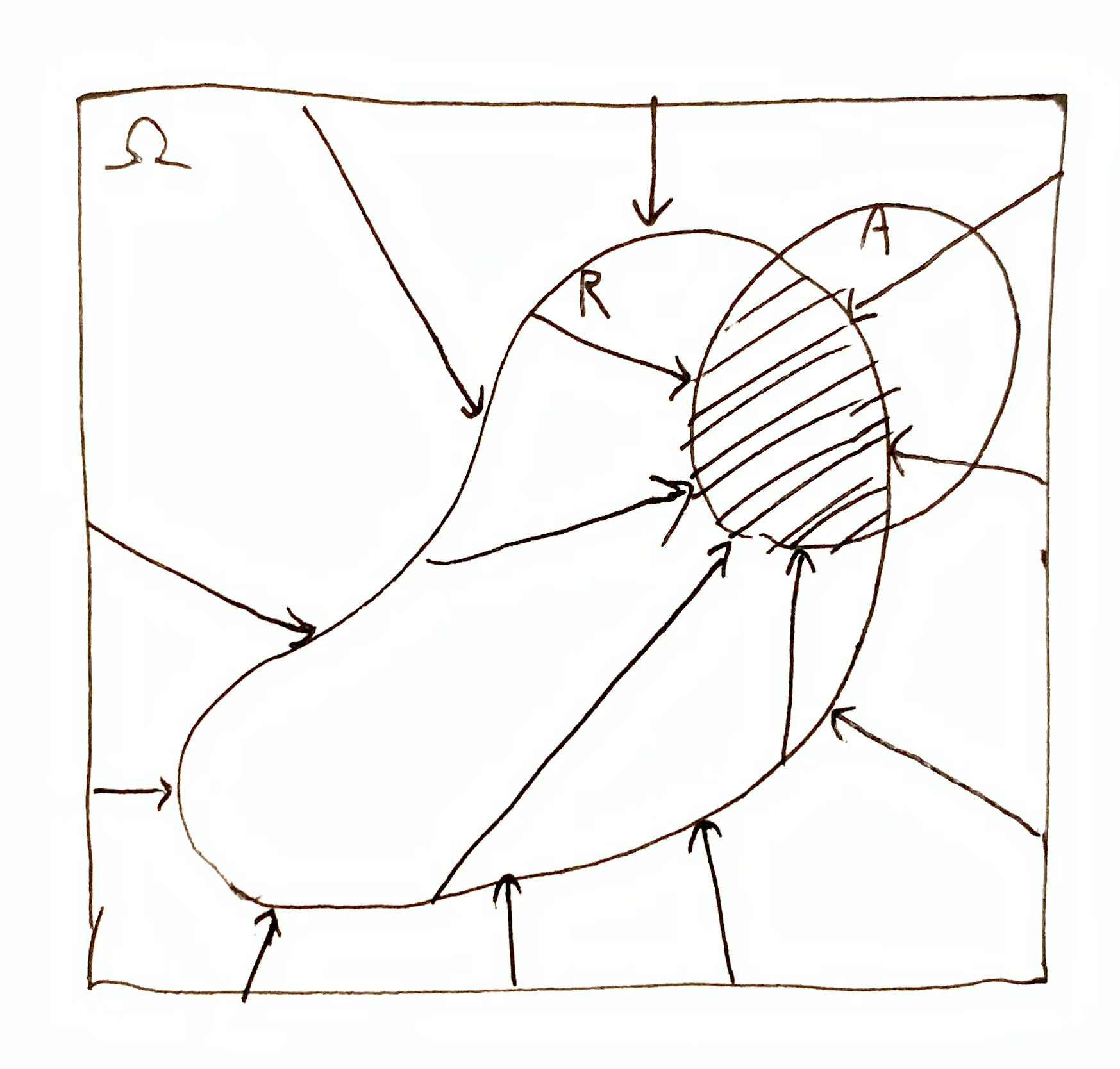
The PMI $i_\O(A, R)$ involves a rescaling of $A\dom{R}$ to $A$, shown visually. The transformation $\tra{\O}{A} \to \tra{R}{A\dom{R}}$, when rescaled covers the distance $i_\O(A, R)$ in the diagram. $h(R \tr A\dom{R})$ covers the remaining distance, which is equivalent to the total distance $h(\O\tr A)$.
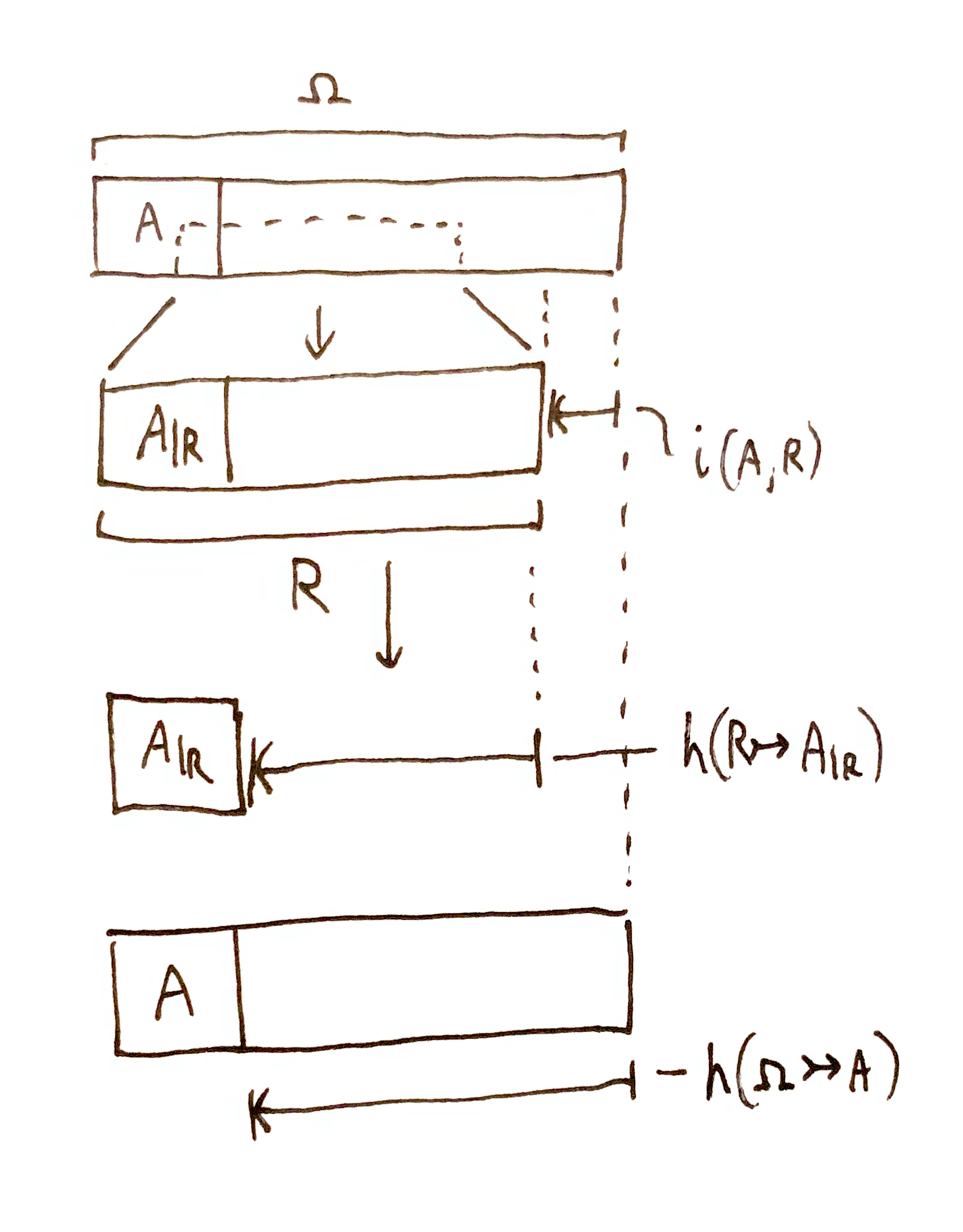
Appendix: PMI Algebra
I’ve played around with an algebraically convenient notation for PMI, and this is what I arrived at:
$$
h(\mi{\O}{A}{R}{A\dom{R}}) \df h(\tra{\O}{A}) - h(\tra{R}{A\dom{R}}) = i_\O(A, R)\,.
$$
It visualizes the joint narrowing down involved in mutual information:
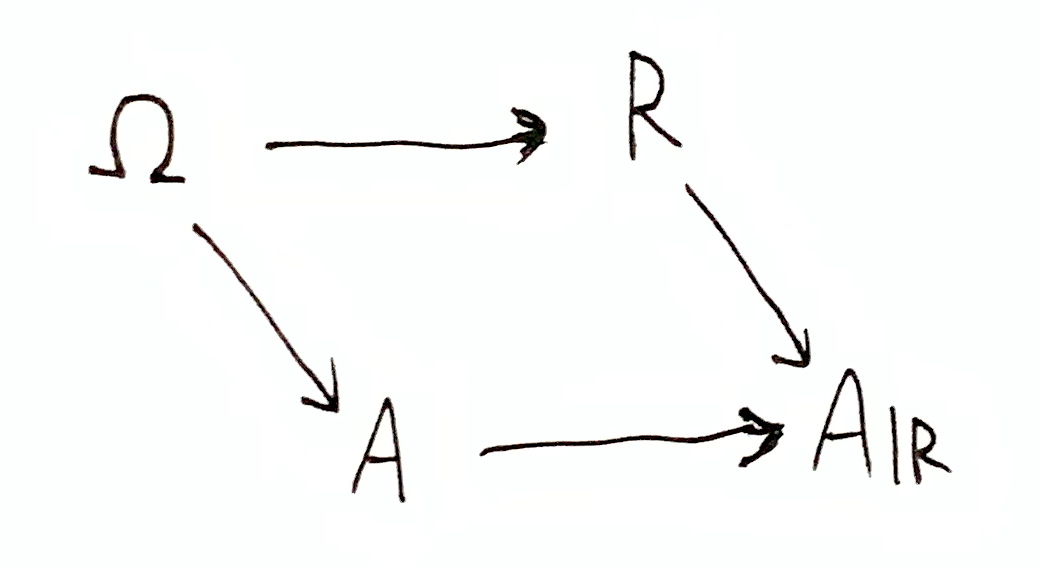
This notation has the downside of not being compact. I’m not sure if it helps with reasoning about relations between quantities. You can evaluate that for yourself:
$h(\mi{\O}{A}{R}{A\dom{R}}) = h(\mi{\O}{R}{A}{A\dom{R}})$
$h(\mi{\O}{A}{R}{A\dom{R}}) = h(\O\tr R) - h(A \tr A\dom{R})$
$h(\O\tr R) - h(\mi{\O}{A}{R}{A\dom{R}}) = h(A \tr A\dom{R})$
$h(\tra{\O}{A}) - h(\mi{\O}{A}{R}{A\dom{R}}) = h(\tra{R}{A\dom{R}})$
$h(\mi{\O}{A}{R}{A\dom{R}}) + h(\tra{R}{A\dom{R}}) = h(\tra{\O}{A})$
$h(\mi{\O}{A}{R}{A\dom{R}}) + h(A \tr A\dom{R}) = h(\O\tr R)$
$h(\mi{\O}{A}{R}{A\dom{R}}) + h(R\tr A\dom{R}) + h(A \tr A\dom{R}) = h(\O\tr A\dom{R})$
$h(\mi{\O}{A}{R}{A\dom{R}}) + h(\O\tr R) + h(R \tr A\dom{R}) = h(\O\tr A\dom{R})$
