[This is a note, which is the seed of an idea and something I’ve written quickly, as opposed to articles that I’ve optimized for readability and transmission of ideas.]
Admittedly my first-pass interaction model in Is The Szilard Cycle Reversible? is not physically realistic. By interaction model, I mean how the particle and piston interact over time. Here I explore some alternative interaction models that try to be more realistic. My main question is whether which-side information is still preserved.
$$
\newcommand{\0}{\mathrm{false}}
\newcommand{\1}{\mathrm{true}}
\newcommand{\mb}{\mathbb}
\newcommand{\mc}{\mathcal}
\newcommand{\mf}{\mathfrak}
\newcommand{\ms}{\mathscr}
\newcommand{\and}{\wedge}
\newcommand{\or}{\vee}
\newcommand{\es}{\emptyset}
\newcommand{\a}{\alpha}
\newcommand{\t}{\tau}
\newcommand{\T}{\Theta}
\newcommand{\D}{\Delta}
\newcommand{\d}{\delta}
\newcommand{\o}{\omega}
\newcommand{\O}{\Omega}
\newcommand{\x}{\xi}
\newcommand{\z}{\zeta}
\newcommand{\fa}{\forall}
\newcommand{\ex}{\exists}
\newcommand{\X}{\mc{X}}
\newcommand{\Y}{\mc{Y}}
\newcommand{\Z}{\mc{Z}}
\newcommand{\P}{\Psi}
\newcommand{\y}{\psi}
\newcommand{\p}{\phi}
\newcommand{\l}{\lambda}
\newcommand{\L}{\Lambda}
\newcommand{\G}{\Gamma}
\newcommand{\g}{\gamma}
\newcommand{\B}{\mb{B}}
\newcommand{\m}{\times}
\newcommand{\N}{\mb{N}}
\newcommand{\I}{\mb{I}}
\newcommand{\H}{\mc{H}}
\newcommand{\R}{\mb{R}}
\newcommand{\s}{\sigma}
\newcommand{\e}{\varepsilon}
\newcommand{\set}[1]{\left\{#1\right\}}
\newcommand{\par}[1]{\left(#1\right)}
\newcommand{\vtup}[1]{\left\langle#1\right\rangle}
\newcommand{\abs}[1]{\left\lvert#1\right\rvert}
\newcommand{\inv}[1]{{#1}^{-1}}
\newcommand{\ceil}[1]{\left\lceil#1\right\rceil}
\newcommand{\dom}[1]{_{\mid #1}}
\newcommand{\df}{\overset{\mathrm{def}}{=}}
\newcommand{\M}{\mc{M}}
\newcommand{\up}[1]{^{(#1)}}
\newcommand{\Dt}{{\Delta t}}
\newcommand{\tr}{\rightarrowtail}
\newcommand{\qed}{\ \ \blacksquare}
\newcommand{\c}{\overline}
\newcommand{\dg}{\dagger}
\newcommand{\dd}{\mathrm{d}}
\newcommand{\pd}{\partial}
$$
The physically realistic thing to do would be to make the piston an inertial body, meaning that it has its own momentum. If the particle is doing work on the piston by pushing it, then the piston must be climbing a potential gradient. Then, as an inertial body, the piston should fall back down the gradient when not being pushed.
I also tried settling this matter by going to the source: Szilard’s original paper. Szilard specifies that the piston is forcibly moved by an operator. This can be modeled as a wall that moves in a predefined way, regardless of its interaction with the particle. That is certainly easier to model on a computer.
Szilard specifies that the expansion is isothermal, which means the particle regains lost KE (on average) by interacting with oscillating particles in the walls of the container. However, I am modeling the expansion as isentropic to avoid the issue of environmental noise (see Why Doesn't Uncopying Defeat The 2nd Law?). That means the particle does not exchange KE with the walls of the container, and so the particle loses net KE over time.
Inertial Piston Model
Like last time I am modeling this in one spatial dimension. The piston and particle each have one position coordinate. The container has a length, with “caps” on each end.
If the piston is pushing a mass $M$ up against gravity, then the potential field has a constant slope $g$. Then the motion of the piston is described by $M \ddot{x}=-g$, which gives us a parabola (think ball thrown in the air).
The particle experiences no forces, except for elastic collisions with the walls of the container and the piston. We can use the 1D elastic collision formula:
$$
\pmatrix{u_f\\v_f}=\frac{1}{M+m}\pmatrix{M-m & 2m \\ 2M & m-M}\pmatrix{u_i\\v_i}
$$
where $M$ is the mass of the piston (i.e. the mass it is pushing), $m$ is the mass of the particle, $v_i,v_f$ are the initial and final velocities of the particle before and after the collision, and $u_i,u_f$ are the initial and final velocities of the piston before and after collision.
When the particle collides with a fixed wall, its velocity sign changes, i.e. $v_f = -v_i$.
To have the particle push the piston slowly over the course of many back-and-forth bounces, the piston’s mass should be greater than the particle’s, and the particle’s velocity should be greater than piston.
For example, here is a simulation with the following settings Blue is the particle’s trajectory, and orange is the piston’s trajectory. The particle bounces off both the piston and the fixed wall at position -1. The behavior of the combined system is locally chaotic, and globally seems to oscillate.
piston: (mass) $M=1$ and (initial velocity) $u_0 = 0$
particle: (mass) $m = 1/10$ and (initial velocity) $v_0=5$
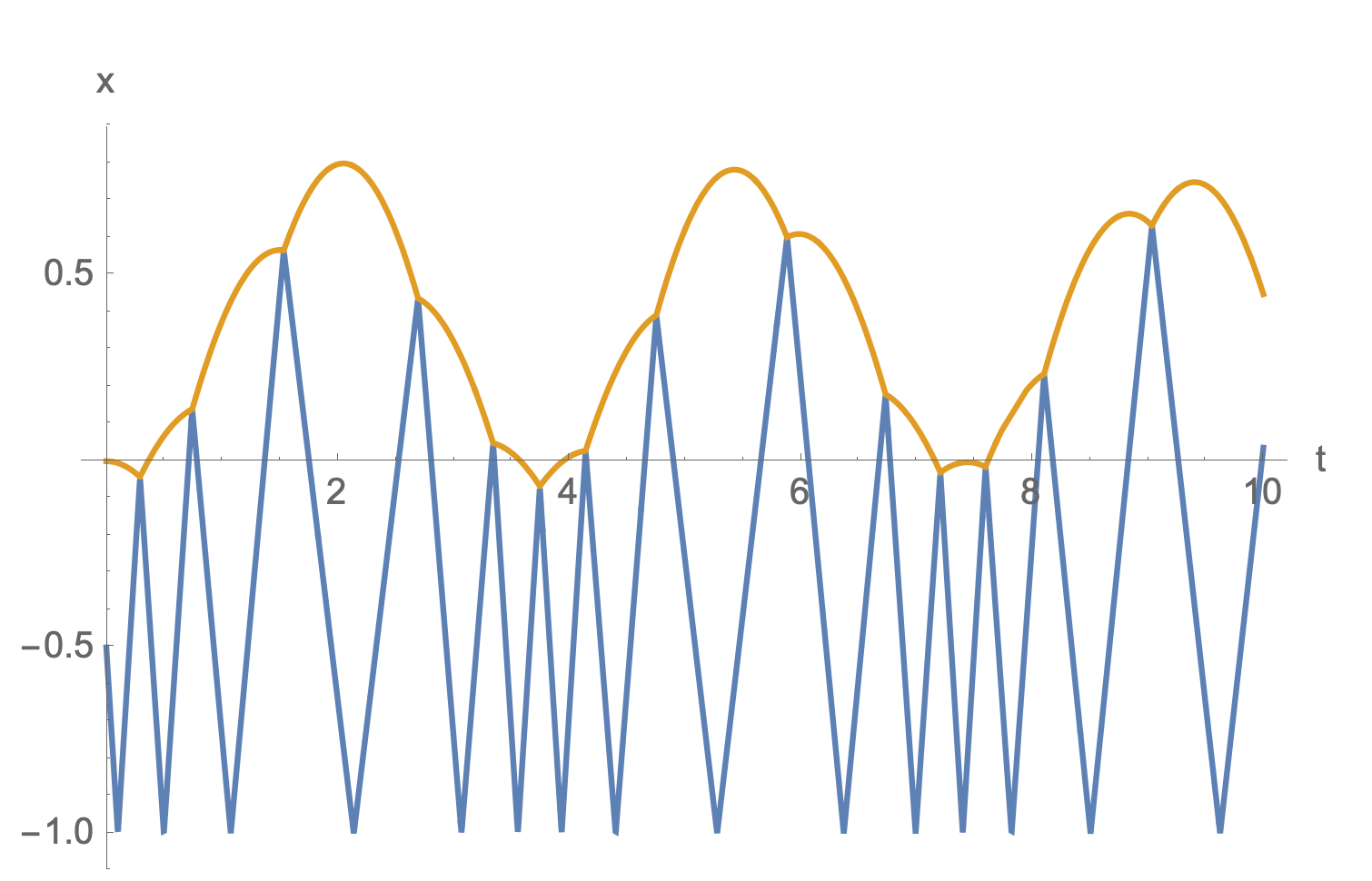
With a much lower particle mass and much higher initial particle velocity, we see less chaotic behavior and a more stable oscillation:
piston: (mass) $M=1$ and (initial velocity) $u_0 = 0$
particle: (mass) $m = 1/100$ and (initial velocity) $v_0=20$
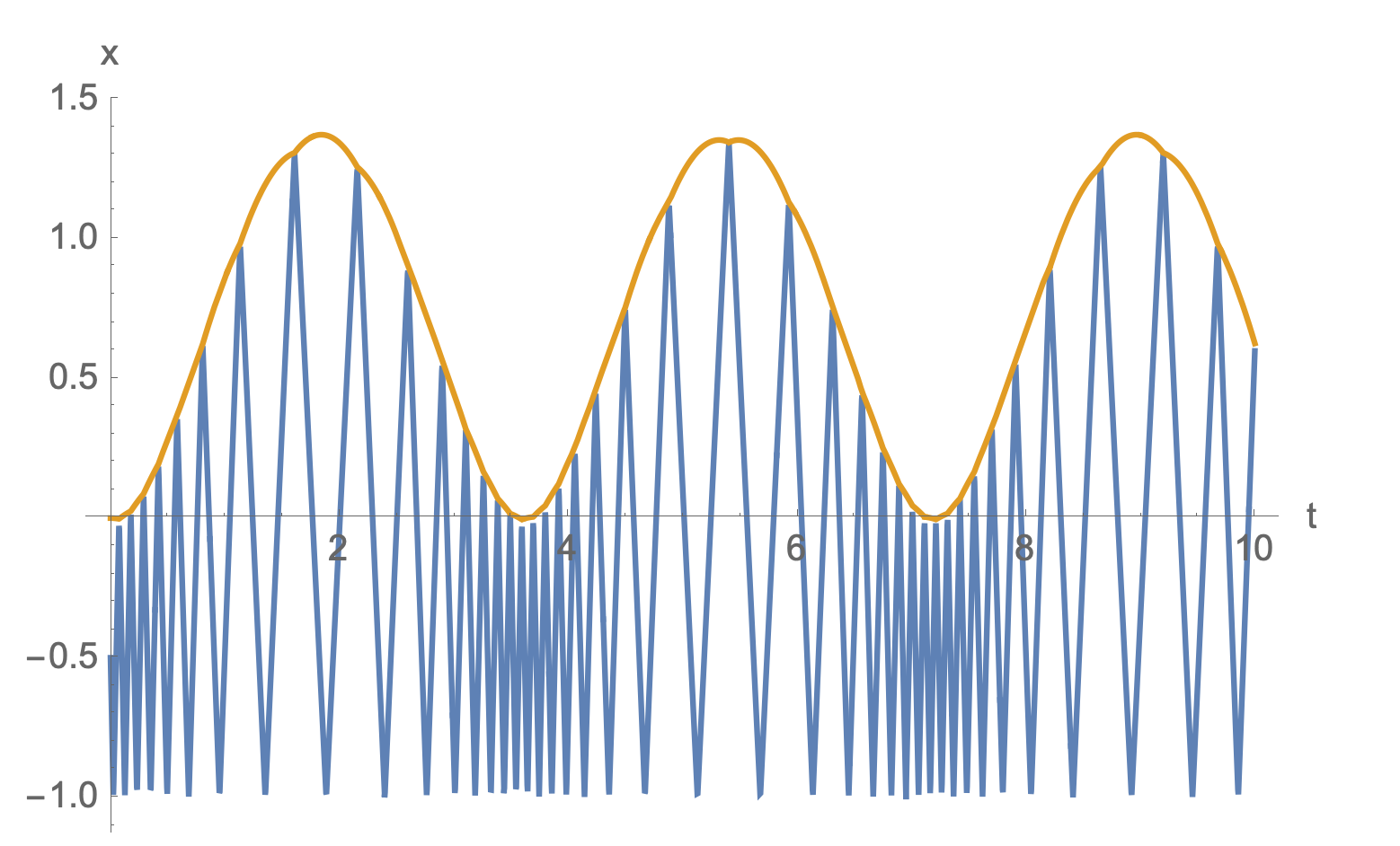
To avoid this sort of oscillation, I should have the piston mass decrease as it is pushed up, corresponding to adiabatic (isentropic) expansion, where the entropy of the gas remains fixed as it expands. The gas does not absorb thermal energy from its container, and so it cools as it transfers KE to the piston. In order to maintain approximate equilibrium through out the change (making it a quasistatic process), the piston mass is slowly decreased so that the gas pressure and piston force opposing it always in balance.
I tried running the same simulation where the piston mass is the following function of the container length: $M(L)=M_0\cdot\par{\frac{L_0}{L}}^\gamma$ where $\gamma=1$. I got this formula from the ideal gas isentropic relation between pressure and volume: $\frac{P_f}{P_i}=\par{\frac{V_i}{V_f}}^\gamma$. Pressure of a single particle applied to a point (end of the 1D container) is just its force, and the volume of the 1D container is its length. This resulted in very similar looking particle-piston trajectories as before, with oscillatory behavior. I suspect I would need to have the piston mass decrease as it is pushed up the potential slope, but not increase as it falls down the potential slope.
At any rate, a quick workaround is to fix the piston in place once it reaches its maximally expanded position. Like this:
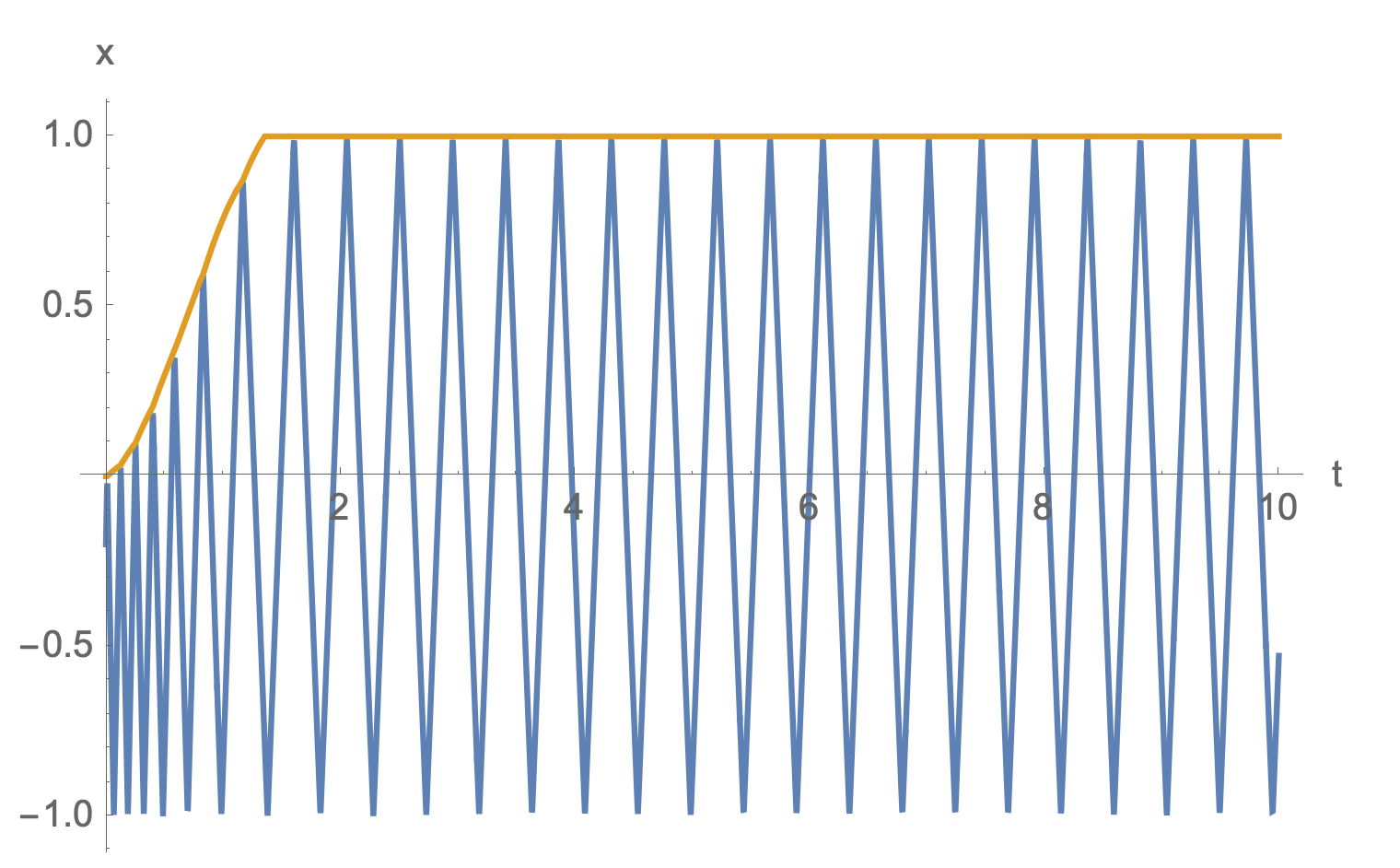
Like in Is The Szilard Cycle Reversible?, I sampled a thousand initial particle states on each side of the container - left side as red and right side as blue.
It seems that this too results in disjoint state regions, and so the which-side information is again preserved. What’s also apparent is that the state regions are shrinking. Liouville’s theorem guarantees that state volume will be conserved in a closed system. However, here there is energy being lost to the piston. If we plotted the joint state space of the particle and piston we would see that the total state region does not shrink.
Since the particle’s state region is shrinking, that implies there is state uncertainty being moved into the piston dimension. What does that imply about the reversibility of this process? A process is thermodynamically reversible if both the system undergoing the process and its environment can be reset to their joint initial state. If uncertainty is transferred from the particle to the piston (piston’s state region has increased in volume), is that reversible? Since all of the transferred uncertainty is accumulating in a single degree of freedom (the total energy absorbed from the particle), it should be possible in principle to transfer that uncertainty back to the particle. It is only when uncertainty becomes spread out among many degrees of freedom (like heat transfer from many particles to many particles) that this transfer becomes irreversible (why? - An exercise left to the reader).
Controlled Piston Model
Particles colliding with moving walls
When you forcibly move a wall into particles, you transfer KE to them. This is why compressing a gas adds heat energy (average KE) to the gas.
The time reversal of this process is forcibly expanding a gas by pulling the wall away from the particles. This must result in KE extraction from the particles.
We see this bear out in the low-level Newtonian mechanics of collision with the formula $v_f = 2u-v_i$, where $v_i$ is the incoming (initial) velocity of the particle before wall collision, $v_f$ is the outgoing (final) velocity of the particle after wall collision, and $u$ is the fixed velocity of the wall.
This formula can be derived from the one-dimensional elastic collision formula (see #Inertial Piston Model) by taking the mass of the wall to infinity (reference):
Taking the limit as $m_u \to \infty$, we get
$$
\lim_{M\to\infty}\frac{1}{M+m}\pmatrix{M-m & 2m \\ 2M & m-M} = \pmatrix{1 & 0 \\ 2 & -1}
$$
giving us
$$
\pmatrix{u_f\\v_f}=\pmatrix{1 & 0 \\ 2 & -1}\pmatrix{u_i\\v_i} = \pmatrix{u_i\\2u_i-v_i}
$$
where $u=u_i=u_v$.
Simulation
In this simulation the piston has infinite mass and moves along a predefined path, representing an external operator controlling the movement of the piston. The particle collides elastically with the piston using the formula $v_f = 2u-v_i$, where $u$ is the velocity of the piston. If the piston is moving away from the particle (in the same direction as $v_i$), we see that $\abs{v_f}<\abs{v_i}$ and so the particle loses KE.
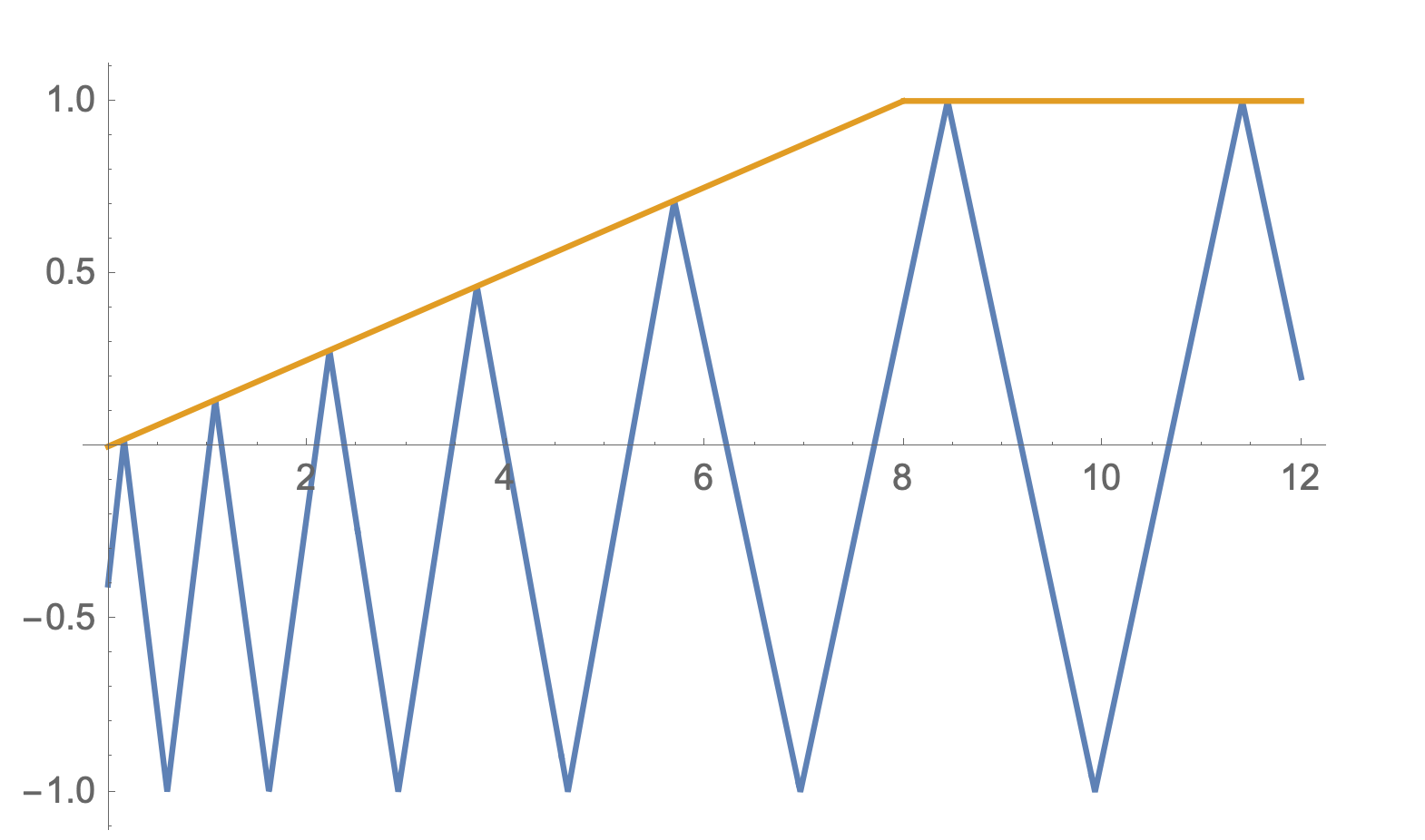
An example particle trajectory (blue) with a piston (orange) moving along a predefined path. When the particle collides with the moving piston it loses KE.
Here I sample an ensemble of initial particles. The blue particles bounce off the blue piston and the red particles bounce off the red piston. Since the blue and red pistons follow the same path for all particles (of the same color), I can visualize the pistons superimposed on the ensemble. Since the piston’s predefined movement depends on which side (which color) the particle is on, this controll “program” requires the which-side bit stored in memory.
Clearly the state regions overlap over time, and so the which-side information is no longer present in the particle system at the end of the piston expansion.
Question: Why do some interaction models preserve which-side information, while other interaction models do not?
